파동 방정식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 파동 방정식의 형태
4. 파동 방정식의 해법
5. 추가 정보
참조

1. 개요

파동 방정식은 파동의 진동을 수학적으로 표현하는 편미분 방정식으로, 현악기의 파동 문제 연구에서 시작되었다. 일반적으로 ${\partial^2 u \over \partial t^2 } = c^2 \nabla^2u$ 형태로 표현되며, 여기서 c는 파동의 속도, u는 파동의 진폭을 나타낸다. 파동 방정식은 선형 미분 방정식이므로 중첩의 원리가 적용되며, 푸리에 변환을 통해 분석할 수 있다. 1차원, 2차원, 3차원 등 다양한 형태가 존재하며, 매질의 진동 현상뿐만 아니라 전자기파 등에도 적용된다. 파동 방정식의 해는 달랑베르의 해법, 변수 분리법, 푸리에 변환, 그린 함수 등을 통해 구할 수 있으며, 경계 조건과 비선형성을 고려한 다양한 응용 분야가 존재한다.

더 읽어볼만한 페이지

파동 - 진동수
진동수는 주기적인 현상이 단위 시간당 반복되는 횟수를 나타내는 물리량으로, 주기와 역수 관계를 가지며 소리의 높낮이, 빛의 색깔 등을 결정하는 중요한 요소이다.
파동 - 전파
전파는 전기장과 자기장의 결합으로 공간을 통해 이동하는 전자기파의 일종으로, 통신, 방송 등 다양한 분야에서 활용되며, 파장에 따라 분류되고, 열적 및 비열적 효과를 가지며 생물학적 영향을 미칠 수 있다.
편미분 방정식 - 나비에-스토크스 방정식
나비에-스토크스 방정식은 유체의 운동을 기술하는 비선형 편미분방정식으로, 질량 및 운동량 보존 법칙에 기반하며, 해의 존재성과 매끄러움은 밀레니엄 문제이지만 다양한 유체 흐름 모델링과 수치 해석적 응용에 활용된다.
편미분 방정식 - 슈뢰딩거 방정식
슈뢰딩거 방정식은 양자역학에서 시스템의 시간적 변화를 기술하는 기본 방정식으로, 파동 함수에 대한 편미분 방정식이며, 시스템의 총 에너지를 나타내는 해밀토니안 연산자를 포함하고, 양자 상태를 기술하며, 다양한 양자역학적 현상을 설명하는 데 사용된다.
물리학 개념 - 절연체
절연체는 전기 전도성을 막아 전기의 흐름을 제어하고 안전을 확보하며, 밴드 이론에 따라 큰 띠틈을 가져 외부 전압이 띠틈을 넘어서면 절연 파괴가 발생하며, 유리에서 세라믹, 고분자 복합 재료 등으로 제작되어 전선, 케이블 등 다양한 분야에 사용된다.
물리학 개념 - 전기 전도체
전기 전도체는 전기를 잘 통하는 물질로, 금속, 전해질, 초전도체, 반도체 등이 있으며, 구리, 은, 알루미늄 등 다양한 재료가 전선 등에 사용된다.

파동 방정식
개요
유형	선형 편미분 방정식
영역	물리학, 공학
차수	2차
차원	공간 1, 2, 또는 3차원, 시간 1차원
표기	u = u(x, t) (1차원) u = u(x, y, t) (2차원) u = u(x, y, z, t) (3차원)
형태
1차원 파동 방정식	∂²u/∂t² = v²(∂²u/∂x²)
3차원 파동 방정식	∂²u/∂t² = v²∇²u
일반적인 형태	□u = 0
d'Alembert 연산자	□ = ∂²/∂t² − v²∇²
해	d'Alembert 공식
변수
u	파동의 진폭
t	시간
x	공간 위치
v	파동의 위상 속도
∇²	라플라스 연산자

2. 역사

장 르 롱 달랑베르, 레온하르트 오일러, 다니엘 베르누이, 조제프루이 라그랑주가 떨리는 현악기의 현에서 발생하는 파동 문제를 연구하였다.

3. 파동 방정식의 형태

파동 방정식은 다음과 같은 형태를 가진다.

: ${ \partial^2 u \over \partial t^2 } = c^2 \nabla^2u$

여기서 $c$ 는 파동의 속도를 나타내는 매개변수이다. 예를 들어, 공기 중을 통해 전달되는 음파의 경우 이 값은 대략 300m이며, 이 속도는 음속이라고 불린다. 현의 진동의 경우 $c$ 는 다양한 값을 가질 수 있다.^[17]

$u(\mathbf x,t)$ 는 시간 $t$ 와 위치 $\mathbf x$ 에서 파동의 진폭을 나타내는 함수이다. 예를 들어, 음파의 경우 진폭은 해당 위치의 공기 압력을 나타내며, 진동하는 현의 경우 기준 위치로부터의 변위를 나타낸다. 파동의 종류에 따라 $u$ 는 스칼라 또는 벡터가 될 수 있다. $\nabla^2$ 는 위치 $x$ 에 대한 라플라스 연산자이다.

기본적인 파동 방정식은 선형 미분 방정식이다. 따라서 서로 다른 두 파동을 결합하면 단순히 두 파동을 더한 것과 같다. 또한, 파동을 분석하기 위해 성분별로 나눌 수 있다. 푸리에 변환을 사용하면 파동을 사인 함수들로 분해할 수 있으며, 이는 파동 방정식을 분석하는 데 유용하다.

1차원, 2차원, 3차원에서의 파동 방정식은 다음과 같다.

차원	방정식
1차원	${ \partial^2 u \over \partial t^2 } = c^2 { \partial^2 u \over \partial x^2 }$
2차원	${ \partial^2 u \over \partial t^2 } = c^2 \left ({ \partial^2 u \over \partial x^2 } + { \partial^2 u \over \partial y^2 } \right )$
3차원	$\frac{1}{s^2}\frac{\partial^2 u}{\partial t^2} = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2}$

식의 상수를 주파수에 따른 변수로 고려하여 더 복잡하고 실제적인 파동 방정식을 만들 수 있다. 이때의 방정식은 비선형이 된다.

파동 방정식은 진행파와 정상파를 포함한 파동을 설명하는 쌍곡선 편미분 방정식이다. 정상파는 반대 방향으로 이동하는 파동의 선형 중첩으로 생각할 수 있다.

3. 1. 1차원 파동 방정식

파동 방정식은 파동의 움직임을 나타내는 방정식이다. 1차원 파동 방정식은 주로 현의 진동과 같은 현상을 설명하는 데 사용된다.

1차원 공간에서 파동 방정식은 다음과 같이 표현된다.

:

\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2}.

이 방정식에서

u

는 시간에 따른 위치

x

에서의 파동의 변위(진폭)를 나타내고,

c

는 파동의 속도를 나타낸다. 이 방정식은 시간

t

외에 공간 차원이

x

하나뿐이므로 1차원 방정식이라고 불린다.

파동 방정식은 현의 진동^[2], 훅의 법칙 등 다양한 물리적 환경에서 유도될 수 있다. 탄성 이론에서 훅의 법칙은 재료의 변형 정도가 변형을 유발하는 힘과 선형적으로 관련되어 있음을 나타낸다.

1차원 파동 방정식은 훅의 법칙으로부터 다음과 같이 유도될 수 있다. 질량

m

의 작은 추들이 질량이 없는 길이

h

의 스프링으로 연결된 배열을 상상해 보자. 스프링은 스프링 상수

k

를 갖는다.

300px

여기서

u(x)

는

x

에 위치한 질량의 평형 위치로부터의 거리를 측정한다. 위치

x+h

에서 질량

m

에 가해지는 힘은 다음과 같다.

:

\begin{align}F_\text{Hooke}  &= F_{x+2h} - F_x = k [u(x + 2h, t) - u(x + h, t)] - k[u(x + h,t) - u(x, t)].\end{align}

위치

x+h

에서 추에 대한 운동 방정식은 다음과 같다.

:

\frac{\partial^2}{\partial t^2} u(x + h, t) = \frac{k}{m} [u(x + 2h, t) - u(x + h, t) - u(x + h, t) + u(x, t)].

추의 배열이 총 질량

M

과 전체 길이

L

에 균등하게 간격을 둔

N

개의 추로 구성되고, 배열의 총 스프링 상수가

K

라면, 위 방정식을 다음과 같이 쓸 수 있다.

:

\frac{\partial^2}{\partial t^2} u(x + h, t) = \frac{KL^2}{M} \frac{[u(x + 2h, t) - 2u(x + h, t) + u(x, t)]}{h^2}.

N \rightarrow \infty

,

h \rightarrow 0

의 극한을 취하면, 다음을 얻는다.

:

\frac{\partial^2 u(x, t)}{\partial t^2} = \frac{KL^2}{M} \frac{\partial^2 u(x, t)}{\partial x^2},

이는 이계도함수의 정의에서 비롯된다.

\frac{KL^2}{M}

는 이 경우의 전파 속도의 제곱이다.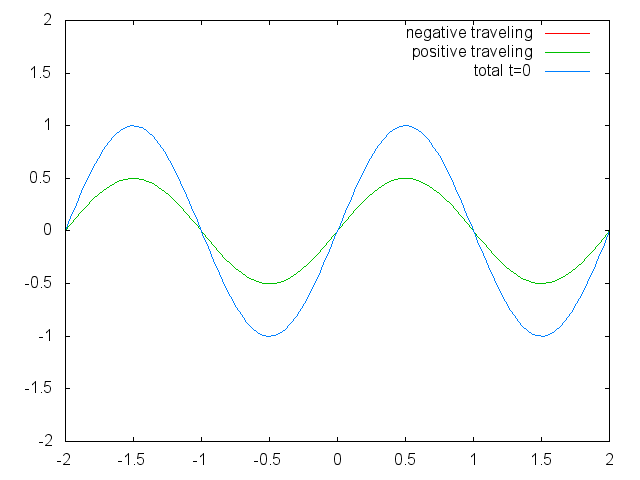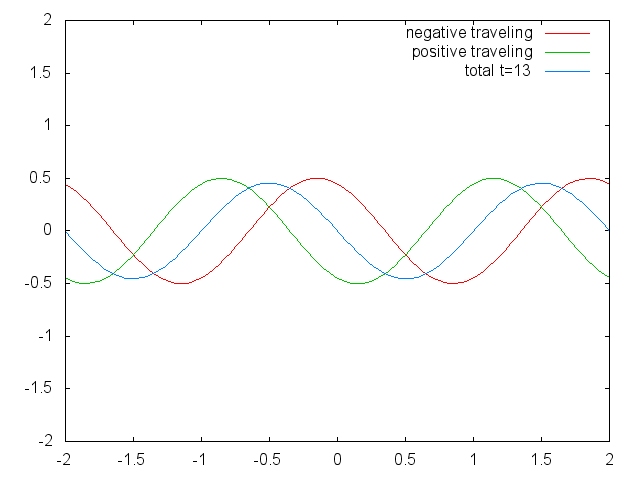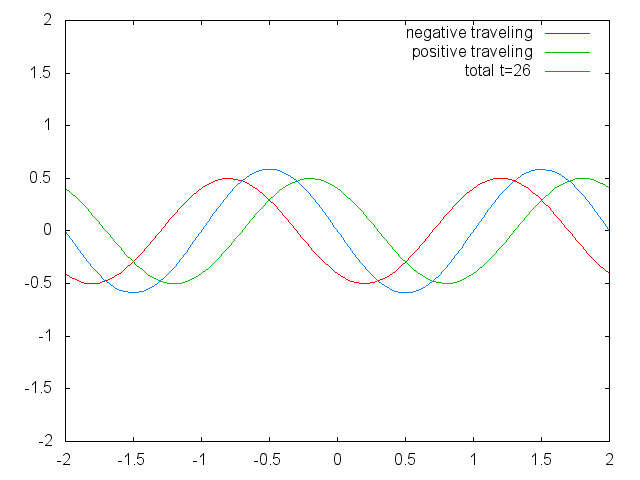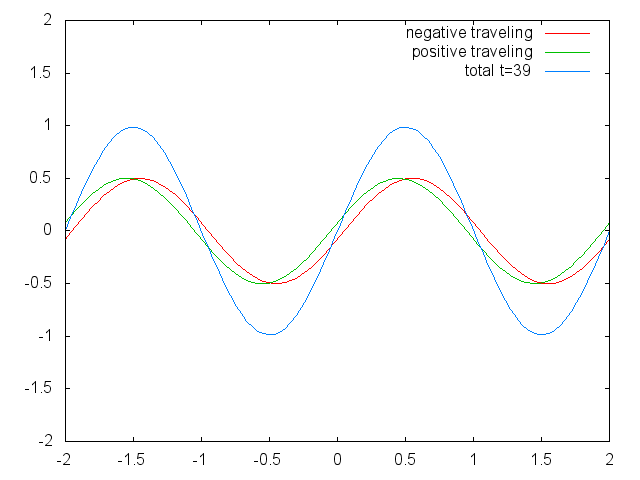

1차원 정상파는 서로 반대 방향으로 이동하는 두 파동의 중첩으로 나타난다.

막대를 따라 전파되는 응력 펄스의 경우, 막대는 무한히 많은 스프링처럼 작용하며 훅의 법칙에 대해 유도된 방정식의 확장으로 간주될 수 있다. 일정한 단면을 가진 균일한 막대는 다음과 같은 강성

K

를 갖는다.

:

K = \frac{EA}{L},

여기서

A

는 단면적이고,

E

는 재료의 영률이다. 파동 방정식은 다음과 같다.

:

\frac{\partial^2 u(x, t)}{\partial t^2} = \frac{EAL}{M} \frac{\partial^2 u(x, t)}{\partial x^2}.

AL

은 막대의 부피이므로

:

\frac{AL}{M} = \frac{1}{\rho},

여기서

\rho

는 재료의 밀도이다. 따라서 파동 방정식은 다음과 같이 축소된다.

:

\frac{\partial^2 u(x, t)}{\partial t^2} = \frac{E}{\rho} \frac{\partial^2 u(x, t)}{\partial x^2}.

따라서 막대 내 응력파의 속도는

\sqrt{E/\rho}

이다.

1차원 파동 방정식은 비교적 간단한 일반해를 구할 수 있다.^[3]

새로운 변수를 다음과 같이 정의하면

:

\begin{align}\xi  &= x - c t, \\\eta &= x + c t\end{align}

파동 방정식은 다음과 같이 변환된다.

:

\frac{\partial^2 u}{\partial \xi \partial \eta}(x, t) = 0,

이는 일반해

:

u(x, t) = F(\xi) + G(\eta) = F(x - c t) + G(x + c t).

를 도출한다.

즉, 해는 오른쪽으로 이동하는 함수

F

와 왼쪽으로 이동하는 함수

G

의 합이다. "이동"은

x

에 대한 개별적인 임의 함수들의 형태가 일정하게 유지되지만, 함수는 시간

c

의 속도로 왼쪽과 오른쪽으로 이동한다는 의미이다. 이는 장 르 롱 달랑베르에 의해 유도되었다.^[4]

초깃값 문제의 경우, 초기 조건을 만족하도록 함수

F

와

G

를 결정할 수 있다.

:

u(x, 0) = f(x),

:

u_t(x, 0) = g(x).

결과는 달랑베르 공식이다.

:

u(x, t) = \frac{f(x - ct) + f(x + ct)}{2} + \frac{1}{2c} \int_{x-ct}^{x+ct} g(s) \, ds.

파동 방정식은 선형 미분 방정식이므로, 중첩의 원리를 따른다. 즉, 둘 이상의 파동에 의해 발생한 순 변위는 각 파동이 개별적으로 발생시켰을 변위의 합이다. 또한, 파동의 동작은 파동을 구성 요소로 분해하여 분석할 수 있다. 예를 들어, 푸리에 변환은 파동을 사인파 성분으로 분해한다.

3차원일 경우 파동 방정식은 다음과 같다.^[17]

:

\frac{1}{s^2}\frac{\partial^2 u}{\partial t^2} = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2}

1차원 파동 방정식은 다음과 같다.^[18]

:

\frac{1}{s^2}\frac{\partial^2 u}{\partial t^2} = \frac{\partial^2 u}{\partial x^2}

3. 2. 2차원 파동 방정식

2차원에서의 파동 방정식은 다음과 같다.

:

{ \partial^2 u \over \partial t^2 } = c^2 \left ({ \partial^2 u \over \partial x^2 } + { \partial^2 u \over \partial y^2 } \right )

^[17]

여기서

u(x, y, t)

는 시간

t

와 위치

(x, y)

에서 파동의 진폭을 나타낸다.

식의 상수를 주파수에 따른 변수로 생각하여 더 복잡하고 실제적인 파동 방정식을 만들 수도 있는데, 이때의 방정식은 비선형이 된다.

2차원 공간에서 파동 방정식은 다음과 같이 표현된다.

u_{tt} = c^2 \left( u_{xx} + u_{yy} \right).

이 문제는 3차원 이론을 사용하여

u

를 세 번째 차원에 독립적인 3차원 함수로 간주하면 해결할 수 있다. 초기 조건이 다음과 같을 때,

u(0,x,y)=0, \quad u_t(0,x,y) = \phi(x,y),

3차원 해 공식은 다음과 같다.

u(t,x,y) = tM_{ct}[\phi] = \frac{t}{4\pi} \iint_S \phi(x + ct\alpha,\, y + ct\beta) \, d\omega,

여기서

\alpha

와

\beta

는 단위 구면의 처음 두 좌표이고,

d\omega

는 구면의 면적 요소이다. 이 적분은 중심이

(x, y)

이고 반지름이

ct

인 원판

D

에 대한 이중 적분으로 다시 쓸 수 있다.

u(t,x,y) = \frac{1}{2\pi c} \iint_D \frac{\phi(x+\xi, y +\eta)}{\sqrt{(ct)^2 - \xi^2 - \eta^2}} d\xi \, d\eta.

(t, x, y)

에서의 해는 빛 원뿔

(x -\xi)^2 + (y - \eta)^2 = c^2 t^2 ,

상의 데이터뿐만 아니라 그 원뿔 내부에 있는 데이터에도 의존한다.

2차원 파동 방정식은 주로 막의 진동^[18] 현상을 기술하는데 사용된다. 진동·파동 현상은 일반적으로 현, 막, 공기, 물 등 매질의 진동 현상을 가리키며 주로 유체역학, 탄성체역학에서 다룬다.

3. 3. 3차원 파동 방정식

3차원 파동 방정식은 다음과 같이 표현된다.^[1]

:

\frac{\partial^2 u}{\partial t^2} = c^2 \left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2}\right)

여기서

`c`는 파동의 전파 속도를 나타내는 고정된 음이 아닌 실수 계수이다.
`u`는 변위 또는, 더 일반적으로, 보존된 양(예: 압력 또는 밀도)을 나타내는 스칼라장이다.
`x`, `y` 및 `z`는 세 개의 공간 좌표이고 `t`는 시간 좌표이다.

이 방정식은 임의의 점에서,

u

의 시간에 대한 2차 도함수는 공간에 대한

u

의 2차 도함수의 합에 비례하며, 비례 상수는 파동 속도의 제곱이라고 말한다.

벡터 미적분학의 표기법을 사용하면, 파동 방정식은 다음과 같이 간결하게 쓸 수 있다.

:

u_{tt} = c^2 \Delta u,

또는

:

\Box u = 0,

여기서 이중 아래 첨자는 시간에 대한 2차 편도함수를 나타내고,

\Delta

는 라플라스 연산자이며

\Box

는 달랑베르 연산자이며, 다음과 같이 정의된다.

:

u_{tt} = \frac{\partial^2 u}{\partial t^2}, \qquad \Delta = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} +  \frac{\partial^2}{\partial z^2}, \qquad \Box = \frac{1}{c^2} \frac{\partial^2}{\partial t^2} - \Delta.

이 (양방향) 파동 방정식의 해는 매우 복잡할 수 있다. 그래도, 다양한 전파 방향과 파장을 가지지만 모두 동일한 전파 속도 `c`를 갖는 정현파 평면파의 선형 결합으로 분석할 수 있다. 이 분석이 가능한 이유는 파동 방정식이 선형 미분 방정식이고 동차적이기 때문에, 해의 임의의 배수도 해이고, 임의의 두 해의 합도 다시 해이기 때문이다. 이 속성은 물리학에서 중첩 원리라고 불린다.

파동 방정식만으로는 물리적인 해를 특정할 수 없다. 고유한 해는 일반적으로 파동의 진폭과 위상을 규정하는 초기 조건과 같은 추가 조건으로 문제를 설정하여 얻습니다. 또 다른 중요한 종류의 문제는 경계 조건으로 지정된 폐쇄된 공간에서 발생하며, 여기서 해는 정상파 또는 고조파를 나타내며, 이는 악기의 고조파와 유사하다.

3차원 공간에서 파동 방정식에 대한 초기값 문제의 해는 구면파에 대한 해당 해로부터 얻을 수 있다. 그 결과는 2차원 공간에서 동일한 해를 얻는 데에도 사용될 수 있다.

## 푸리에 변환

푸리에 변환을 적용하여 일정한 주파수를 갖는 해를 얻을 수 있다.

:

\Psi(\mathbf{r}, t) = \int_{-\infty}^\infty \Psi(\mathbf{r}, \omega) e^{-i\omega t} \, d\omega,

이는 파동 방정식을 다음과 같은 형태의 타원형 편미분 방정식으로 변환한다.

:

\left(\nabla^2 + \frac{\omega^2}{c^2}\right) \Psi(\mathbf{r}, \omega) = 0.

이는 헬름홀츠 방정식이며, 변수 분리법을 사용하여 풀 수 있다. 구면 좌표계에서 이 방법을 사용하면 반경 방향 변수와 각도 변수가 분리되어 해를 다음과 같이 쓸 수 있다.^[10]

:

\Psi(\mathbf{r}, \omega) = \sum_{l,m} f_{lm}(r) Y_{lm}(\theta, \phi).

해의 각도 부분은 구면 조화 함수의 형태를 가지며, 반경 방향 함수는 다음을 만족한다.

:

\left[\frac{d^2}{dr^2} + \frac{2}{r} \frac{d}{dr} + k^2 - \frac{l(l + 1)}{r^2}\right] f_l(r) = 0.

`m`에 독립적이며,

k^2=\omega^2 / c^2

이다.

:

f_{l}(r)=\frac{1}{\sqrt{r}}u_{l}(r),

를 대입하면 방정식은 다음과 같이 변환된다.

:

\left[\frac{d^2}{dr^2} + \frac{1}{r} \frac{d}{dr} + k^2 - \frac{(l + \frac{1}{2})^2}{r^2}\right] u_l(r) = 0,

이것은 베셀 방정식이다.

## 구면파

`l = 0`인 경우를 생각해 보자. 그러면 각 의존성이 없어지고 진폭은 반경 거리에만 의존한다. 즉, `Ψ(r, t) → u(r, t)`이다. 이 경우 파동 방정식은 다음과 같이 축소된다

:

\left(\frac{\partial^2}{\partial r^2} + \frac{2}{r} \frac{\partial}{\partial r} - \frac{1}{c^2} \frac{\partial^2}{\partial t^2}\right) u(r, t) = 0.

이 방정식은 다음과 같이 다시 쓸 수 있다.

:

\frac{\partial^2(ru)}{\partial t^2} - c^2 \frac{\partial^2(ru)}{\partial r^2} = 0,

여기서 양 `ru`는 1차원 파동 방정식을 만족한다. 따라서 다음과 같은 형태의 해가 있다.

:

u(r, t) = \frac{1}{r} F(r - ct) + \frac{1}{r} G(r + ct),

여기서 `F`와 `G`는 1차원 파동 방정식의 일반적인 해이며 각각 발산하는 구면파와 수렴하는 구면파로 해석할 수 있다. 발산하는 파동은 점원에 의해 생성될 수 있으며, `r`이 증가함에 따라 진폭이 감소하는 것 외에는 형태가 변경되지 않는 날카로운 신호를 가능하게 한다(상단 오른쪽에 있는 구면파의 그림 참조). 이러한 파동은 홀수 차원의 공간의 경우에만 존재한다.

각 의존성을 갖는 3차원 파동 방정식의 해의 물리적 예는 쌍극자 복사를 참조하십시오.

"단색"이라는 단어는 정확하지는 않지만, 잘 정의된 주파수를 가진 빛 또는 전자기파를 지칭하기 때문에, 그 정신은 3차원 파동 방정식의 고유 모드를 찾는 것이다. 이전 절 푸리에 변환의 유도를 따라, 만약 우리가 해를 잘 정의된 ''상수'' 각주파수 `ω`로 시간에 따라 진동하는 구면파로 제한한다면, 변환된 함수 `ru(r, t)`는 단순히 평면파 해를 갖는다:

:

r u(r, t) = Ae^{i(\omega t \pm kr)},

또는

:

u(r, t) = \frac{A}{r} e^{i(\omega t \pm kr)}.

이로부터 우리는 구면파 진동의 최대 세기, 즉 제곱된 파동 진폭으로 특징지어지는

:

I = |u(r, t)|^2 = \frac

3. 4. 벡터 파동 방정식

벡터 파동 방정식은 무한소 부피 요소에 힘의 평형을 적용하여 얻을 수 있다. 매질이 부피 요소 내에서 균질(즉,

\mathbf{x}

에 의존하지 않음)인 탄성 계수

E

를 갖는 경우, 응력 텐서는

\mathbf{T} = E \nabla \mathbf{u}

로 주어진다. 여기서

\mathbf{u}(\mathbf{x}, t)

는 벡터 탄성 변위이다. 다음의 국부 평형을 고려한다.

# 변위

\mathbf{u}

로 인한 장력

\operatorname{div} \mathbf{T} = \nabla\cdot(E \nabla \mathbf{u}) = E \Delta\mathbf{u}

# 국부 가속도

\partial^2\mathbf{u} / \partial t^2

로 인한 관성력

\rho \partial^2\mathbf{u}/\partial t^2

이 둘은

\rho \frac{\partial^2 \mathbf{u}}{\partial t^2} - E \Delta \mathbf{u} = \mathbf{0}.

으로 쓸 수 있다.^[7]

밀도

\rho

와 탄성 계수

E

를 병합하면 음속

c = \sqrt{E/\rho}

가 된다. 이를 삽입하면, 균질 매질에 대한 파동 방정식은 다음과 같다.^[7]

:

\frac{\partial^2 \mathbf{u}}{\partial t^2} - c^2 \Delta \mathbf{u} = \boldsymbol{0}.

위의 2차 벡터 편미분 방정식은 두 개의 상호 독립적인 해를 제공한다. 이차 속도 항

c^2 = (+c)^2 = (-c)^2

에서 두 파동이 반대 방향

+c

와

-c

로 이동할 수 있다.

\nabla\mathbf{c} = \mathbf{0}

의 경우, 달랑베르 연산자를 사용한 특수한 이중 파동 방정식은 다음과 같다.^[8]

:

\left(\frac{\partial}{\partial t} - \mathbf{c} \cdot \nabla\right)\left(\frac{\partial}{\partial t} + \mathbf{c} \cdot \nabla \right) \mathbf{u} =\left(\frac{\partial^2}{\partial t^2} + (\mathbf{c} \cdot \nabla)^2\right) \mathbf{u} = \mathbf{0}.

\nabla \mathbf{c} = \mathbf{0}

인 경우, 이는 다음과 같이 단순화된다.

:

\left(\frac{\partial^2}{\partial t^2} + c^2\Delta\right) \mathbf{u} = \mathbf{0}.

따라서, 미리 정의된 전파 방향

\mathbf{c}

으로 이동하는 파동을 갖는 벡터 1차 일방향 파동 방정식은 다음과 같다.^[9]

:

\frac{\partial \mathbf{u}}{\partial t} - \mathbf{c} \cdot \nabla \mathbf{u} = \mathbf{0}.

탄성파 방정식 (또는 Navier–Cauchy 방정식)은 3차원에서 등방성 균질 탄성 매질 내 파동의 전파를 설명한다. 대부분의 고체 재료는 탄성이 있으므로 이 방정식은 지진파와 같은 현상을 설명하며, 재료의 결함을 감지하는 데 사용되는 초음파와 같은 현상을 설명한다. 이 방정식은 종파 및 횡파 운동을 모두 고려해야 하므로 위에 주어진 방정식보다 더 복잡한 형태를 가지고 있다.

:

\rho \ddot{\mathbf{u}} = \mathbf{f} + (\lambda + 2\mu) \nabla(\nabla \cdot \mathbf{u}) - \mu\nabla \times (\nabla \times \mathbf{u}),

여기서:

$\lambda$ 및 $\mu$ 는 매질의 탄성 특성을 설명하는 소위 라메 상수이다.
$\rho$ 는 밀도이다.
$\mathbf{f}$ 는 소스 함수(구동력)이다.
$\mathbf{u}$ 는 변위 벡터이다.

탄성파 방정식에서 힘과 변위는 모두 벡터 양이다. 따라서 이 방정식은 때때로 벡터 파동 방정식이라고도 한다.

4. 파동 방정식의 해법

1차원 파동 방정식을 푸는 방법 중 하나는 주파수 고유 모드를 분석하는 것이다. 고유 모드는 잘 정의된 상수 각주파수 ω로 시간에 따라 진동하는 해이며, 파동 함수의 시간 부분은 $e^{-i\omega t} = \cos(\omega t) - i \sin(\omega t)$ 형태를 취한다. 진폭은 공간 변수 x의 함수 f(x)이므로, 파동 함수에 대해 변수 분리를 할 수 있다.^[6]

: $u_\omega(x, t) = e^{-i\omega t} f(x).$

이는 공간 부분 f(x)에 대한 상미분 방정식을 유도한다.^[6]

: $\frac{\partial^2 u_\omega }{\partial t^2} = \frac{\partial^2}{\partial t^2} \left(e^{-i\omega t} f(x)\right) = -\omega^2 e^{-i\omega t} f(x) = c^2 \frac{\partial^2}{\partial x^2} \left(e^{-i\omega t} f(x)\right).$

따라서

: $\frac{d^2}{dx^2}f(x) = -\left(\frac{\omega}{c}\right)^2 f(x),$

이는 f(x)에 대한 고유값 방정식이며, 헬름홀츠 방정식으로 알려져 있다. 이 방정식은 평면파 해를 갖는다.^[6]

: $f(x) = A e^{\pm ikx},$

여기서 파수 k = ω/c 이다.

고유 모드에 대한 전체 파동 함수는 다음과 같은 선형 결합이다.^[6]

: $u_\omega(x, t) = e^{-i\omega t} \left(A e^{-ikx} + B e^{ikx}\right) = A e^{-i (kx + \omega t)} + B e^{i (kx - \omega t)},$

여기서 복소수 A, B는 문제의 초기 및 경계 조건에 따라 결정된다.

각 고유 모드는 위상 인자 $e^{-i\omega t}$ 로 시간에 따라 변화하므로, 고유 모드 전개를 통해 파동 방정식의 완전한 해를 구할 수 있다.^[6]

: $u(x, t) = \int_{-\infty}^\infty s(\omega) u_\omega(x, t) \, d\omega,$

또는 평면파로 표현하면 다음과 같다.^[6]

: $\begin{align}u(x, t) &= \int_{-\infty}^\infty s_+(\omega) e^{-i(kx+\omega t)} \, d\omega + \int_{-\infty}^\infty s_-(\omega) e^{i(kx-\omega t)} \, d\omega \\&= \int_{-\infty}^\infty s_+(\omega) e^{-ik(x+ct)} \, d\omega + \int_{-\infty}^\infty s_-(\omega) e^{ik (x-ct)} \, d\omega \\&= F(x - ct) + G(x + ct),\end{align}$

이는 달랑베르의 해법과 같은 형태이다. 함수 s_±(ω)는 푸리에 성분으로, 초기 및 경계 조건에 의해 결정된다. 이는 주파수 영역 방법이며, FDTD 방법과 같은 시간 영역에서의 직접적인 전파와 달리 파동 묶음 u(x, t)를 표현하는 데 완전하며, 시간 팽창이 없는 파동을 나타내는 데 완전하다. 처프 파동 해는 ω의 시간 변화를 허용하여 시간 팽창이 있는 파동을 표현할 수 있다.^[6]

4. 1. 달랑베르의 해법

1차원 파동 방정식의 경우 비교적 간단한 일반해를 구할 수 있다. 새로운 변수를 다음과 같이 정의하면^[3]

\begin{align}\xi  &= x - c t, \\\eta &= x + c t\end{align}

파동 방정식은 다음과 같이 변환된다.

\frac{\partial^2 u}{\partial \xi \partial \eta}(x, t) = 0,

이는 일반해

u(x, t) = F(\xi) + G(\eta) = F(x - c t) + G(x + c t).

를 도출한다.

다시 말해, 해는 오른쪽으로 이동하는 함수 와 왼쪽으로 이동하는 함수 의 합이다. "이동"은 에 대한 개별적인 임의 함수들의 형태가 일정하게 유지되지만, 함수는 시간 의 속도로 왼쪽과 오른쪽으로 이동한다는 의미이다. 이는 장 르 롱 달랑베르에 의해 유도되었다.^[4]

이 결과를 얻는 또 다른 방법은 두 개의 1차 미분 연산자를 사용하여 파동 방정식을 인수분해하는 것이다.

\left[\frac{\partial}{\partial t} - c\frac{\partial}{\partial x}\right] \left[\frac{\partial}{\partial t} + c\frac{\partial}{\partial x}\right] u = 0.

그 다음, 원래 방정식에 대해

v \equiv \frac{\partial u}{\partial t} + c\frac{\partial u}{\partial x},

로 정의할 수 있으며, 다음을 만족해야 함을 알 수 있다.

\frac{\partial v}{\partial t} - c\frac{\partial v}{\partial x} = 0.

이 이류 방정식은 방향으로의 의 방향 도함수가 0이라고 해석하여 풀 수 있다. 이는 의 값이 형태의 특성선에서 일정하다는 것을 의미하며, 따라서 는 에만 의존해야 하며, 즉 형태를 가져야 한다. 그런 다음, 를 와 관련시키는 첫 번째 (비제차) 방정식을 풀기 위해, 위와 유사한 논리로, 그 제차해는 형태의 함수여야 함을 알 수 있다. 형태의 특수해를 추측하면 다음과 같다.

\left[\frac{\partial}{\partial t} + c\frac{\partial}{\partial x}\right] G(x + ct) = H(x + ct).

좌변을 전개하고, 항을 재정렬한 다음, 변수 변환 를 사용하면 방정식이 다음과 같이 간단해진다.

G'(s) = \frac{H(s)}{2c}.

이는 적분을 통해 원하는 형태의 특수해 를 찾을 수 있다는 것을 의미한다. 따라서, 가 을 따른다는 것을 다시 한 번 보였다.^[5]

초깃값 문제의 경우, 임의 함수 와 는 초기 조건을 만족하도록 결정될 수 있다.

u(x, 0) = f(x),

u_t(x, 0) = g(x).

결과는 달랑베르 공식이다.

u(x, t) = \frac{f(x - ct) + f(x + ct)}{2} + \frac{1}{2c} \int_{x-ct}^{x+ct} g(s) \, ds.

고전적인 의미에서, 이고 이면, 이다. 그러나 파형 와 는 델타 함수와 같은 일반화 함수일 수도 있다. 이 경우, 해는 오른쪽 또는 왼쪽으로 이동하는 임펄스로 해석될 수 있다.

기본 파동 방정식은 선형 미분 방정식이므로, 중첩의 원리를 따른다. 이는 둘 이상의 파동에 의해 발생한 순 변위가 각 파동이 개별적으로 발생시켰을 변위의 합이라는 것을 의미한다. 또한, 파동의 동작은 파동을 구성 요소로 분해하여 분석할 수 있다. 예를 들어, 푸리에 변환은 파동을 사인파 성분으로 분해한다.

4. 2. 변수 분리법

헬름홀츠 방정식을 사용하여 1차원 파동 방정식을 푸는 또 다른 방법은 먼저 주파수 고유 모드를 분석하는 것이다. 고유 모드는 잘 정의된 '상수' 각 주파수 ω로 시간에 따라 진동하는 해로서, 파동 함수의 시간 부분은

e^{-i\omega t} = \cos(\omega t) - i \sin(\omega t)

의 형태를 취하고, 진폭은 공간 변수 x의 함수 f(x)이므로 파동 함수에 대한 변수 분리를 제공한다.^[6]

:

u_\omega(x, t) = e^{-i\omega t} f(x).

이는 공간 부분 f(x)에 대한 상미분 방정식을 생성한다.^[6]

:

\frac{\partial^2 u_\omega }{\partial t^2} = \frac{\partial^2}{\partial t^2} \left(e^{-i\omega t} f(x)\right) = -\omega^2 e^{-i\omega t} f(x) = c^2 \frac{\partial^2}{\partial x^2} \left(e^{-i\omega t} f(x)\right).

따라서

:

\frac{d^2}{dx^2}f(x) = -\left(\frac{\omega}{c}\right)^2 f(x),

이는 정확히 f(x)에 대한 고유값 방정식이므로 고유 모드라는 이름이 붙었다. 헬름홀츠 방정식으로 알려진 이 방정식은 잘 알려진 평면파 해를 갖는다.^[6]

:

f(x) = A e^{\pm ikx},

파수 k = ω/c를 갖는다.

이 고유 모드에 대한 전체 파동 함수는 다음과 같은 선형 결합이다.^[6]

:

u_\omega(x, t) = e^{-i\omega t} \left(A e^{-ikx} + B e^{ikx}\right) = A e^{-i (kx + \omega t)} + B e^{i (kx - \omega t)},

여기서 복소수 A, B는 일반적으로 문제의 초기 및 경계 조건에 따라 달라진다.

고유 모드는 파동 방정식의 완전한 해를 구성하는 데 유용한데, 그 이유는 각 고유 모드가 위상 인자

e^{-i\omega t}

로 시간에 따라 자명하게 진화하므로 완전한 해를 고유 모드 전개로 분해할 수 있기 때문이다.^[6]

:

u(x, t) = \int_{-\infty}^\infty s(\omega) u_\omega(x, t) \, d\omega,

또는 평면파로 표현하면 다음과 같다.^[6]

:

\begin{align}u(x, t) &= \int_{-\infty}^\infty s_+(\omega) e^{-i(kx+\omega t)} \, d\omega + \int_{-\infty}^\infty s_-(\omega) e^{i(kx-\omega t)} \, d\omega \\&= \int_{-\infty}^\infty s_+(\omega) e^{-ik(x+ct)} \, d\omega + \int_{-\infty}^\infty s_-(\omega) e^{ik (x-ct)} \, d\omega \\&= F(x - ct) + G(x + ct),\end{align}

이는 달랑베르의 해법과 정확히 동일한 형태이다. 함수 s_±(ω)는 푸리에 성분으로 알려져 있으며 초기 및 경계 조건에 의해 결정된다. 이는 시간 영역에서의 직접적인 전파, 예를 들어 FDTD 방법과 같은, 주파수 영역 방법이며, 파동 묶음 u(x, t)을 표현하는 데 완전하며, 시간 팽창이 없는 파동을 나타내는 데 완전하다. 시간 팽창이 있는 파동을 표현하기 위한 푸리에 전개의 완전성은 ω의 시간 변화를 허용하는 처프 파동 해에 의해 도전받았다.^[6] 처프 파동 해는 특히 flyby anomaly의 매우 크지만 이전에 설명할 수 없었던 레이더 잔류물에 의해 암시되는 것으로 보이며, 사인파 해와 달리, 소스의 과거 처프 상태에 해당하는 비례적으로 이동된 주파수 및 시간 팽창에서만 어떤 거리에서든 수신 가능하다.^[6]

4. 3. 푸리에 변환

푸리에 변환을 이용해 파동은 사인 함수들로 쪼개어질 수 있으며, 이 방법은 파동 방정식을 분석하는 데 유용하다.^[3] 기본 파동 방정식은 선형 미분 방정식이므로, 중첩의 원리를 따른다. 즉, 둘 이상의 파동에 의해 발생한 순 변위는 각 파동이 개별적으로 발생시켰을 변위의 합이다. 또한, 파동의 동작은 파동을 구성 요소로 분해하여 분석할 수 있다. 예를 들어, 푸리에 변환은 파동을 사인파 성분으로 분해한다.

1차원 파동 방정식을 푸는 또 다른 방법은 먼저 주파수 고유 모드를 분석하는 것이다. 고유 모드는 잘 정의된 '상수' 각 주파수 ω로 시간에 따라 진동하는 해로서, 파동 함수의 시간 부분은

e^{-i\omega t}

의 형태를 취하고, 진폭은 공간 변수 x의 함수 f(x)이므로 파동 함수에 대한 변수 분리를 제공한다.

:

u_\omega(x, t) = e^{-i\omega t} f(x).

이는 공간 부분 f(x)에 대한 상미분 방정식을 생성한다.

:

\frac{\partial^2 u_\omega }{\partial t^2} = \frac{\partial^2}{\partial t^2} \left(e^{-i\omega t} f(x)\right) = -\omega^2 e^{-i\omega t} f(x) = c^2 \frac{\partial^2}{\partial x^2} \left(e^{-i\omega t} f(x)\right).

따라서

:

\frac{d^2}{dx^2}f(x) = -\left(\frac{\omega}{c}\right)^2 f(x),

이는 정확히 f(x)에 대한 고유값 방정식이므로 고유 모드라는 이름이 붙었다. 헬름홀츠 방정식으로 알려진 이 방정식은 잘 알려진 평면파 해를 갖는다.

:

f(x) = A e^{\pm ikx},

파수 k = ω/c를 갖는다.

이 고유 모드에 대한 전체 파동 함수는 다음과 같은 선형 결합이다.

:

u_\omega(x, t) = e^{-i\omega t} \left(A e^{-ikx} + B e^{ikx}\right) = A e^{-i (kx + \omega t)} + B e^{i (kx - \omega t)},

여기서 복소수 A, B는 일반적으로 문제의 초기 및 경계 조건에 따라 달라진다.

고유 모드는 파동 방정식의 완전한 해를 구성하는 데 유용한데, 그 이유는 각 고유 모드가 위상 인자

e^{-i\omega t}

로 시간에 따라 자명하게 진화하므로 완전한 해를 고유 모드 전개로 분해할 수 있기 때문이다.

:

u(x, t) = \int_{-\infty}^\infty s(\omega) u_\omega(x, t) \, d\omega,

또는 평면파로 표현하면 다음과 같다.

:

\begin{align}u(x, t) &= \int_{-\infty}^\infty s_+(\omega) e^{-i(kx+\omega t)} \, d\omega + \int_{-\infty}^\infty s_-(\omega) e^{i(kx-\omega t)} \, d\omega \\&= \int_{-\infty}^\infty s_+(\omega) e^{-ik(x+ct)} \, d\omega + \int_{-\infty}^\infty s_-(\omega) e^{ik (x-ct)} \, d\omega \\&= F(x - ct) + G(x + ct),\end{align}

이는 대수적 접근 방식과 정확히 동일한 형태이다. 함수 s_±(ω)는 푸리에 성분으로 알려져 있으며 초기 및 경계 조건에 의해 결정된다. 이는 시간 영역에서의 직접적인 전파 (예: FDTD 방법)와 같은, 주파수 영역 방법이며, 파동 묶음 u(x, t)를 표현하는 데 완전하며, 시간 팽창이 없는 파동을 나타내는 데 완전하다. 시간 팽창이 있는 파동을 표현하기 위한 푸리에 전개의 완전성은 ω의 시간 변화를 허용하는 처프 파동 해에 의해 도전받았다.^[6] 처프 파동 해는 특히 flyby anomaly의 매우 크지만 이전에 설명할 수 없었던 레이더 잔류물에 의해 암시되는 것으로 보이며, 사인파 해와 달리, 소스의 과거 처프 상태에 해당하는 비례적으로 이동된 주파수 및 시간 팽창에서만 어떤 거리에서든 수신 가능하다.

푸리에 변환을 적용하여 일정한 주파수를 갖는 해를 얻을 수 있다.

:

\Psi(\mathbf{r}, t) = \int_{-\infty}^\infty \Psi(\mathbf{r}, \omega) e^{-i\omega t} \, d\omega,

이는 파동 방정식을 다음과 같은 형태의 타원형 편미분 방정식으로 변환한다.

:

\left(\nabla^2 + \frac{\omega^2}{c^2}\right) \Psi(\mathbf{r}, \omega) = 0.

이는 헬름홀츠 방정식이며, 변수 분리법을 사용하여 풀 수 있다.

푸리에 변환에 의해,

:

\hat G (\omega)=  \frac{1}{-\omega_0^2 + \omega_1^2 + \cdots + \omega_D^2},\quad G(t, x) = \frac{1}{(2\pi)^{D+1}} \int \hat G(\omega) e^{+i \omega_0 t + i \vec \omega \cdot \vec x}d\omega_0 d\vec\omega.

\omega_0

항은 잔류 정리에 의해 적분될 수 있다. 부적절 적분이기 때문에 적분을

+i\epsilon

또는

-i\epsilon

로 약간 방해해야 한다. 하나의 방해는 순방향 해를 제공하고, 다른 하나는 역방향 해를 제공한다.^[11] 순방향 해는 다음과 같다.

:

G(t,x) = \frac{1}{(2\pi)^D} \int  \frac{\sin (\|\vec \omega\| t)}{\|\vec \omega\|} e^{i \vec \omega \cdot \vec x}d\vec \omega,\quad\partial_t G(t, x) = \frac{1}{(2\pi)^D} \int  \cos(\|\vec \omega\| t) e^{i \vec \omega \cdot \vec x}d\vec \omega.

적분은 푸아송 핵을 해석적으로 연장하여 해결할 수 있으며,^[12]^[13]

:

G(t, x) = \lim _{\epsilon \rightarrow 0^{+}} \frac{C_D}{D-1}\operatorname{Im}\left[\|x\|^2-(t-i \epsilon)^2\right]^{-(D-1) / 2}

여기서

C_D=\pi^{-(D+1) / 2} \Gamma((D+1) / 2)

는

(D + 1)

차원 초구의 표면적의 절반이다.^[13]

4. 4. 그린 함수

1+D

차원에서 비균질 파동 방정식은 다음과 같다.

:

(\partial_{tt} - c^2\nabla^2) u = s(t, x)

시간을 재조정하여 파동 속도를

c = 1

로 설정할 수 있다.

파동 방정식

(\partial_{tt} - \nabla^2) u = s(t, x)

는 시간에 대해 2차이므로, 임펄스 응답에는 가속도 임펄스와 속도 임펄스 두가지가 있다. 가속도 임펄스를 가하는 효과는 파동 속도

\partial_t u

를 갑자기 변화시키는 것이고, 속도 임펄스를 가하는 효과는 파동 변위

u

를 갑자기 변화시키는 것이다.

가속도 임펄스의 경우,

s(t,x) = \delta^{D+1}(t,x)

이며, 여기서

\delta

는 디랙 델타 함수이다. 이 경우의 해는 파동 방정식에 대한 그린 함수

G

라고 불린다.

속도 임펄스의 경우,

s(t, x) = \partial_t \delta^{D+1}(t,x)

이므로, 그린 함수

G

를 풀면 이 경우의 해는 단순히

\partial_t G

이다.

그린 함수의 주요 용도는 초기값 문제를 뒤아멜의 원리를 통해 푸는 것이며, 이는 동차 및 비동차 경우 모두에 적용된다.

그린 함수

G

와 초기 조건

u(0,x), \partial_t u(0,x)

가 주어지면, 동차 파동 방정식의 해는 다음과 같다.^[12]

:

u = (\partial_t G) \ast u + G \ast \partial_t u

여기서 별표는 공간에서의 합성곱을 나타낸다. 더 구체적으로는 다음과 같다.

:

u(t, x) = \int  (\partial_t G)(t, x-x') u(0, x') dx' +  \int  G(t, x-x') (\partial_t u)(0, x') dx'.

비동차인 경우, 해는 시공간에 대한 합성곱에 의해 하나의 항을 더 가진다.

:

\iint_{t' < t} G(t-t', x-x') s(t', x')dt' dx'.

푸리에 변환에 의해 다음과 같이 표현된다.

:

\hat G (\omega)=  \frac{1}{-\omega_0^2 + \omega_1^2 + \cdots + \omega_D^2}, \quad G(t, x) = \frac{1}{(2\pi)^{D+1}} \int \hat G(\omega) e^{+i \omega_0 t + i \vec \omega \cdot \vec x}d\omega_0 d\vec\omega.

\omega_0

항은 잔류 정리에 의해 적분될 수 있다. 부적절 적분이기 때문에 적분을

+i\epsilon

또는

-i\epsilon

로 약간 방해해야 한다. 하나의 방해는 순방향 해를 제공하고, 다른 하나는 역방향 해를 제공한다.^[11] 순방향 해는 다음과 같다.

:

G(t,x) = \frac{1}{(2\pi)^D} \int  \frac{\sin (\|\vec \omega\| t)}{\|\vec \omega\|} e^{i \vec \omega \cdot \vec x}d\vec \omega, \quad \partial_t G(t, x) = \frac{1}{(2\pi)^D} \int  \cos(\|\vec \omega\| t) e^{i \vec \omega \cdot \vec x}d\vec \omega.

적분은 푸아송 핵을 해석적으로 연장하여 해결할 수 있으며,^[12]^[13] 다음과 같다.

:

G(t, x) = \lim _{\epsilon \rightarrow 0^{+}} \frac{C_D}{D-1} \operatorname{Im}\left[\|x\|^2-(t-i \epsilon)^2\right]^{-(D-1) / 2}

여기서

C_D=\pi^{-(D+1) / 2} \Gamma((D+1) / 2)

는

(D + 1)

차원 초구의 표면적의 절반이다.^[13]

D

차원에서 그린 함수는

D+n

차원의 그린 함수와 관련될 수 있다.^[14]

함수

s(t, x)

와

(1+D)

차원에서의 미분 방정식의 해

u(t, x)

가 주어졌을 때, 추가적인

n

차원을 상수로 설정하여 이를

(1+D+n)

차원으로 쉽게 확장할 수 있다.

:

s(t, x_{1:D}, x_{D+1:D+n}) = s(t, x_{1:D}), \quad u(t, x_{1:D}, x_{D+1:D+n}) = u(t, x_{1:D}).

그린 함수는

f

와

u

로부터 구성되므로,

(1+D+n)

차원의 그린 함수는

(1+D)

차원의 그린 함수로 적분된다.

:

G_D(t, x_{1:D}) = \int_{\R^n} G_{D+n}(t, x_{1:D}, x_{D+1:D+n}) d^n x_{D+1:D+n}.

D

차원의 그린 함수는

D+2

차원의 그린 함수와 관련될 수 있다. 구면 대칭성에 의해 다음과 같다.

:

G_D(t, r) = \int_{\R^2} G_{D+2}(t, \sqrt{r^2 + y^2 + z^2}) dydz.

극좌표로 적분하면 다음과 같다.

:

G_D(t, r) = 2\pi \int_0^\infty G_{D+2}(t, \sqrt{r^2 + q^2}) qdq = 2\pi \int_r^\infty G_{D+2}(t, q') q'dq',

마지막 등식에서 변수

q' = \sqrt{r^2 + q^2}

로 치환했다. 따라서, 다음과 같은 재귀 관계를 얻는다.

:

G_{D+2}(t, r) = -\frac{1}{2\pi r} \partial_r G_D(t, r).

5. 추가 정보

호이겐스 원리는 파동 방정식에 대한 초기값 문제의 해가 주어진 점에서 뒤로 그려진 광원뿔이 교차하는 구의 데이터에만 의존하고, 그 내부에는 의존하지 않는다는 것을 보여준다. 이는 공간 차원이 홀수일 때만 성립하며, 짝수 차원에서는 파면 뒤의 영역 전체가 0이 아닌 웨이크가 발생한다.^[14] 아다마르의 추측은 파동 방정식의 계수가 일정하지 않더라도 이 원리가 홀수 차원에서 성립한다고 주장하지만, 엄밀히 말하면 특정 계열에 대해서만 정확하다.^[15]

파동 방정식의 해는 일반적으로 초기 조건과 경계 조건으로 지정된 닫힌 공간에서 발생하며, 이는 정상파나 고조파를 나타낸다.^[2] 예를 들어, 양 끝이 고정된 줄의 진동은 경계 조건에 따라 다양한 해를 가질 수 있으며, 슈트름-리우빌 이론을 통해 분석할 수 있다. 2차원 공간에서 드럼헤드의 진동 모드는 헬름홀츠 방정식을 통해, 3차원 공간에서 구의 진동 모드는 구면 조화 함수와 베셀 함수를 통해 나타낼 수 있다.

서로 다른 매질 경계면에서 파동은 일부 투과하고 일부 반사된다. 이때 반사율과 투과율은 두 매질의 파동 속도에 따라 결정되며, 파동 속도가 느린 매질에서 빠른 매질로 진행할 때 반사파는 180°의 반사 위상 변화를 겪는다.

기본 파동 방정식은 선형 미분 방정식이지만, 상수를 주파수에 따른 변수로 생각하면 비선형 파동 방정식을 얻을 수 있다.

5. 1. 호이겐스 원리

Huygens' principe|호이겐스 원리^nl는 파동 방정식에 대한 초기값 문제의 해가 주어진 점, 즉

(t, x, y, z)

에서의 해가

(t, x, y, z)

에서 뒤로 그려진 '''광원뿔'''이 교차하는 반경

ct

의 구에 대한 데이터에만 의존한다는 것을 보여준다. 이 구의 내부에 있는 데이터에는 의존하지 ''않는다''. 따라서 구의 내부는 해에 대한 라쿠나이다. 이 현상을 '''호이겐스 원리'''라고 한다. 이는 공간 차원의 홀수에서만 참이며, 1차원에서는 적분이 디랙 측도에 대해 간격의 경계에서 수행된다.^[14]

홀수 차원에서, 전방 해는

t = r

에서만 0이 아니다. 차원이 증가함에 따라, 파면의 모양은 점점 더 복잡해지며, 디랙 델타 함수의 고차 도함수를 포함한다. 예를 들어,^[14]

차원 (D)	그린 함수 해 (G_D)
1	$G_1=\frac{1}{2 c} \theta(\tau)$
3	$G_3=\frac{1}{4 \pi c^2} \frac{\delta(\tau)}{r}$
5	$G_5=\frac{1}{8 \pi^2 c^2}\left(\frac{\delta(\tau)}{r^3}+\frac{\delta^{\prime}(\tau)}{c r^2}\right)$
7	$G_7=\frac{1}{16 \pi^3 c^2}\left(3 \frac{\delta(\tau)}{r^4}+3 \frac{\delta^{\prime}(\tau)}{c r^3}+\frac{\delta^{\prime \prime}(\tau)}{c^2 r^2}\right)$

여기서 $\tau = t- r$ 이고, 파동 속도 $c$ 는 복원된다.

짝수 차원에서는 전방 해가 $r \leq t$ 에서 0이 아닌데, 파면 뒤의 전체 영역이 0이 아니게 되며, 이를 웨이크라고 한다. 웨이크는 다음 방정식을 갖는다.^[14]

: $G_{D} (t, x ) = (-1)^{1+D / 2} \frac{1}{(2 \pi)^{D / 2}} \frac{1}{c^D} \frac{\theta(t-r / c)}{\left(t^2-r^2 / c^2\right)^{(D-1) / 2}}$

파면 자체도 디랙 델타 함수의 점점 더 높은 도함수를 포함한다.

이는 일반적인 호이겐스 원리 – 시공간의 점 $(t, x)$ 에서의 파동 변위가 $(t, x)$ 를 지나는 특성선상의 점들의 상태에만 의존한다 – 가 홀수 차원에서만 성립함을 의미한다. 물리적 해석은 파동에 의해 전송된 신호가 홀수 차원에서는 왜곡되지 않고, 짝수 차원에서는 왜곡된다는 것이다.^[15]

'''아다마르의 추측'''은 파동 방정식의 계수가 더 이상 일정하지 않더라도 이 일반화된 호이겐스 원리가 모든 홀수 차원에서 여전히 성립한다고 주장한다. 이는 엄밀히 말하면 정확하지 않지만, 특정 계열에 대해서는 정확하다.^[15]

5. 2. 경계 조건

파동 방정식의 해는 일반적으로 초기 조건과 함께 경계 조건으로 지정된 닫힌 공간에서 발생하며, 이 해는 정상파 또는 고조파를 나타낸다. 이는 악기의 고조파와 유사하다.^[2]

두 지점 과 사이에 팽팽하게 당겨진 유연한 줄은 및 에 대해 파동 방정식을 만족한다. 경계점에서 는 다양한 경계 조건을 만족할 수 있는데, 일반적인 형태는 다음과 같다.

\begin{align}

u_x(t, 0) + a u(t, 0) &= 0, \\

u_x(t, L) + b u(t, L) &= 0,\end{align}

여기서 와 는 음수가 아니다. 가 끝점(즉, "고정된 끝")에서 사라져야 하는 경우는 각 또는 가 무한대에 접근할 때 이 조건의 극한이다. 변수 분리법을 사용하여 이 문제의 해를 특수한 형태 로 찾을 수 있다.

그 결과는 다음과 같다.

\frac{T''}{c^2 T} = \frac{v''}{v} = -\lambda.

고유값 는 다음 경계값 문제의 자명하지 않은 해가 존재하도록 결정되어야 한다.

\begin{align}v'' + \lambda v = 0,& \\

v'(0) + a v(0) &= 0, \\

v'(L) + b v(L) &= 0.\end{align}

이것은 슈트름-리우빌 이론의 일반적인 문제의 특별한 경우이다. 와 가 양수이면 고유값은 모두 양수이고 해는 삼각 함수이다. 와 에 대한 제곱 적분 가능한 초기 조건을 만족하는 해는 이러한 함수를 적절한 삼각 함수 급수로 전개하여 얻을 수 있다.

1차원 초기 경계값 이론은 임의의 수의 공간 차원으로 확장될 수 있다. 경계 를 가진 차원 공간에서 도메인 를 고려하면, 가 에 있고, 이면 파동 방정식을 만족해야 한다. 의 경계에서 해 는 다음을 만족해야 한다.

\frac{\partial u}{\partial n} + a u = 0,

여기서 은 에 대한 단위 외향 법선이고, 는 에서 정의된 음이 아닌 함수이다. 가 에서 사라지는 경우는 가 무한대에 접근하는 극한 경우이다. 초기 조건은 다음과 같다.

u(0, x) = f(x), \quad u_t(0, x) = g(x),

여기서 와 는 에서 정의된다. 이 문제는 경계 조건을 만족하는 에서 라플라시안의 고유 함수로 와 를 전개하여 해결할 수 있다. 따라서 고유 함수 는 다음을 만족한다.

\nabla \cdot \nabla v + \lambda v = 0

에서,

\frac{\partial v}{\partial n} + a v = 0

에서.

2차원 공간의 경우, 고유 함수는 경계 위에 팽팽하게 당겨진 드럼헤드의 진동 모드로 해석될 수 있다. 가 원인 경우, 이러한 고유 함수는 극각 의 삼각 함수인 각도 성분을 가지며, 이 각도 성분은 반경 성분의 베셀 함수 (정수 차수)에 곱해진다. 자세한 내용은 헬름홀츠 방정식을 참조한다.

경계가 3차원 공간의 구인 경우, 고유 함수의 각도 성분은 구면 조화 함수이고, 반경 성분은 반정수 차수의 베셀 함수이다.

한 매질(파동 속도가 )에서 다른 매질(파동 속도가 )로 진행하는 입사파의 경우, 파동의 일부는 두 번째 매질로 투과하고, 다른 일부는 반대 방향으로 반사되어 첫 번째 매질에 남게 된다. 투과파와 반사파의 진폭은 경계면에서의 연속성 조건을 사용하여 계산할 수 있다.

각진동수 를 갖는 입사파의 성분을 고려하면, 이 성분은 다음과 같은 파형을 갖는다.

u^\text{inc}(x, t) = Ae^{i(k_1 x - \omega t)},\quad A \in \C.

에서 입사파는 두 매질 사이의 경계면 에 도달한다. 따라서, 해당 반사파와 투과파는 다음과 같은 파형을 갖는다.

u^\text{refl}(x, t) = Be^{i(-k_1 x - \omega t)}, \quadu^\text{trans}(x, t) = Ce^{i(k_2 x - \omega t)}, \quadB, C \in \C.

경계면에서의 연속성 조건은 다음과 같다.

u^\text{inc}(0, t) + u^\text{refl}(0, t) = u^\text{trans}(0, t), \quadu_x^\text{inc}(0, t) + u_x^\text{ref}(0, t) = u_x^\text{trans}(0, t).

이로부터 다음 방정식을 얻을 수 있다.

A + B = C, \quadA - B = \frac{k_2}{k_1} C = \frac{c_1}{c_2} C,

그리고 반사율과 투과율은 다음과 같다.

\frac{B}{A} = \frac{c_2 - c_1}{c_2 + c_1}, \quad\frac{C}{A} = \frac{2c_2}{c_2 + c_1}.

일 때, 반사파는 반사 위상 변화 180°를 갖는다. 왜냐하면 이기 때문이다. 에너지 보존은 다음을 통해 확인할 수 있다.

\frac{B^2}{c_1} + \frac{C^2}{c_2} = \frac{A^2}{c_1}.

위의 논의는 의 각진동수에 관계없이 모든 성분에 적용된다.

의 극한의 경우는 움직이지 않는 "고정된 끝"에 해당하며, 의 극한의 경우는 "자유 끝"에 해당한다.

5. 3. 비선형 파동 방정식

기본적인 파동 방정식은 선형 미분 방정식이다. 따라서 서로 다른 두 파동을 결합하면 단순히 두 파를 더한 것과 같다. 또한, 파동을 분석하기 위해 파를 성분별로 나누어도 된다. 푸리에 변환을 이용해 파동은 사인 함수들로 쪼개질 수 있고, 이 방법은 파동 방정식을 분석하는 데 유용하다.

식의 상수를 주파수에 따른 변수로 생각하여 더 복잡하고 실제적인 파동 방정식을 만들 수 있다. 이때의 방정식은 비선형이 된다.

참조

_[1] 서적 Discovering the Principles of Mechanics 1600–1800 https://books.google[...] Birkhäuser 2008
_[2] 서적 Physics for Scientists and Engineers, Volume 1: Mechanics, Oscillations and Waves; Thermodynamics https://books.google[...] Macmillan 2004
_[3] 웹사이트 d'Alembert's Solution http://mathworld.wol[...] MathWorld 2009-01-21
_[4] 간행물 Recherches sur la courbe que forme une corde tenduë mise en vibration https://books.google[...] Histoire de l'académie royale des sciences et belles lettres de Berlin 1747
_[5] 웹사이트 First and second order linear wave equations http://math.arizona.[...]
_[6] 논문 Observational evidence for travelling wave modes bearing distance proportional shifts 2015
_[7] 논문 Spherical One-Way Wave Equation 2021-04
_[8] 논문 One-Way Wave Operator 2022-10
_[9] 논문 Factorized One-way Wave Equations 2021-12
_[10] 서적 Classical Electrodynamics Wiley 1998-08-14
_[11] 웹사이트 The green function of the wave equation http://julian.tau.ac[...] 2024-09-03
_[12] 웹사이트 Greens Functions for the Wave Equation https://users.flatir[...] 2006-12-28
_[13] 간행물 The Laplace Equation and Wave Equation https://link.springe[...] Springer International Publishing 2024-08-20
_[14] 논문 Wakes and waves in N dimensions https://pubs.aip.org[...] 1993-05-01
_[15] 서적 Methods of mathematical physics. 2: Partial differential equations / by R. Courant Wiley-VCH 2009
_[16] 문서 大石 (1989)
_[17] 문서
_[18] 문서 恒藤 (1983)
_[19] 문서

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com